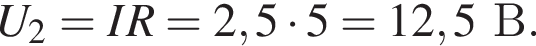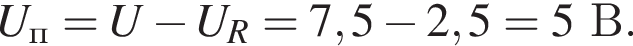В электрической цепи, схема которой приведена на рисунке, сопротивления резисторов R1 = 80 Ом, R2 = 0,12 кОм, R3 = 0,24 кОм, R4 = 0,45 кОм, R5 = 50 Ом, R6 = 35 Ом. Если напряжение на клеммах источника тока U = 48 В, то на резисторе R4 напряжение U4 равно:
В электрической цепи, схема которой приведена на рисунке, сопротивления резисторов R1 = 40 Ом, R2 = 60 Ом, R3 = 0,12 кОм, R4 = 0,36 кОм, R5 = 40 Ом, R6 = 20 Ом. Если напряжение на клеммах источника тока U = 38 В, то на резисторе R5 напряжение U5 равно:
В электрической цепи, схема которой приведена на рисунке, сопротивления резисторов R1 = 50,0 Ом, R2 = 75,0 Ом, R3 = 150 Ом, R4 = 180 Ом, R5 = 20,0 Ом, R6 = 7,00 Ом. Если напряжение на клеммах источника тока U = 18 В, то на резисторе R2 сила тока I2 равна:
В электрической цепи, схема которой приведена на рисунке, сопротивления резисторов R1 = 30,0 Ом, R2 = 45,0 Ом, R3 = 90,0 Ом, R4 = 270 Ом, R5 = 30,0 Ом, R6 = 26,0 Ом. Если напряжение на клеммах источника тока U = 34 В, то на резисторе R5 сила тока I5 равна:
В электрической цепи, схема которой приведена на рисунке, сопротивления резисторов R1 = 80,0 Ом, R2 = 120 Ом, R3 = 80,0 Ом, R4 = 270 Ом, R5 = 30,0 Ом, R6 = 48,0 Ом. Если напряжение на клеммах источника тока U = 21,0 В, то на резисторе R5 сила тока I5 равна:
Если в плоском воздушном конденсаторе, подключённом к источнику постоянного напряжения, расстояние между обкладками увеличить в 3 раза, то энергия электростатического поля конденсатора:
На рисунке изображена схема электрической цепи. Из перечисленного ниже выберите элементы, присутствующие в электрической цепи:
На рисунке изображена схема электрической цепи. Из перечисленного ниже выберите элементы, присутствующие в электрической цепи:
Электрическая цепь, схема которой приведена на рисунке, состоит из источника постоянного тока и трёх резисторов, сопротивления которых R1 = R и R2 = R3 = 2R (см. рис.). Если сила тока, протекающего через резистор с сопротивлением R1, равна І0 , то сила тока І, протекающего через источник тока, равна:
На рисунке изображен участок электрической цепи, напряжение на котором U. Если сопротивление резистора R1 в три раза больше сопротивления резистора R2
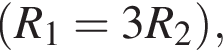 то напряжение U1 на резисторе R1 равно:
то напряжение U1 на резисторе R1 равно:
Электрическая цепь, схема которой приведена на рисунке, состоит из источника постоянного тока и двух резисторов, сопротивления которых одинаковы и равны R (см. рис.). Если сила тока, протекающего через нижний на схеме резистор, равна I0, то сила тока I, протекающего через источник тока, равна:
Электрическая цепь, схема которой приведена на рисунке, состоит из источника постоянного тока и двух резисторов, сопротивления которых одинаковы и равны R (см. рис.). Если сила тока, протекающего через нижний на схеме резистор, равна I0, то сила тока I, протекающего через источник тока, равна:
На рисунке изображен участок электрической цепи, сила тока на котором I. Если сопротивление резистора R1 в два раза больше сопротивления резистора R2 (R1 = 2R2), то сила тока I2 в резисторе R2 равна:
Электрическая цепь, схема которой приведена на рисунке, состоит из источника постоянного тока и двух резисторов, сопротивления которых R и 2R (см. рис.). Если сила тока, протекающего через резистор c сопротивлением R, равна I0, то сила тока I, протекающего через источник тока, равна:
На рисунке изображен участок электрической цепи, напряжение на котором U. Сопротивление резистора R1 в четыре раза больше сопротивления резистора R2
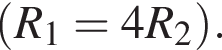 Если напряжение на резисторе R1 равно U1, то напряжение U равно:
Если напряжение на резисторе R1 равно U1, то напряжение U равно:
Электрическая цепь, схема которой приведена на рисунке, состоит из источника постоянного тока и трёх резисторов, сопротивления которых R1 = R и R2 = R3 = 2R (см. рис.). Если сила тока, протекающего через резистор c сопротивлением R1, равна I0, то сила тока I, протекающего через источник тока, равна:
Электрическая цепь, схема которой приведена на рисунке, состоит из источника постоянного тока и двух резисторов, сопротивления которых R и 0,5R (см. рис.). Если сила тока, протекающего через резистор c сопротивлением R, равна I0, то сила тока I, протекающего через источник тока, равна:
На рисунке изображен участок электрической цепи, сила тока на котором I. Сопротивление резистора R1 в пять раз больше сопротивления резистора R2
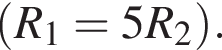 Если сила тока в резисторе R2 равна I2, то сила тока I равна:
Если сила тока в резисторе R2 равна I2, то сила тока I равна:
Электрическая цепь, схема которой приведена на рисунке, состоит из источника постоянного тока и двух резисторов, сопротивления которых R и 0,5R (см. рис.). Если сила тока, протекающего через резистор c сопротивлением 0,5R, равна I0, то сила тока I, протекающего через источник тока, равна:
На рисунке изображен участок электрической цепи, напряжение на котором U. Если сопротивление резистора R2 в два раза больше сопротивления резистора R1
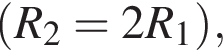 то напряжение U1 на резисторе R1 равно:
то напряжение U1 на резисторе R1 равно:
Лампа и резистор соединены последовательно и подключены к источнику постоянного тока. Сопротивление лампы в десять раз больше, чем сопротивление резистора. Если напряжение на клеммах источника тока U = 22 В, то напряжение на лампе Uл равно:
Лампа и резистор соединены последовательно и подключены к источнику постоянного тока. Сопротивление лампы в десять раз больше, чем сопротивление резистора. Если напряжение на клеммах источника тока U = 220 В, то напряжение на резисторе Uр равно:
Лампа и резистор соединены последовательно и подключены к источнику постоянного тока. Сопротивление лампы в 2,5 раза больше, чем сопротивление резистора. Если напряжение на лампе Uл = 5 В, то напряжение напряжение U на клеммах источника тока равно:
Лампа и резистор соединены последовательно и подключены к источнику постоянного тока. Сопротивление резистора в 5 раз меньше, чем сопротивление лампы. Если напряжение на лампе Uл = 10 В, то напряжение напряжение U на клеммах источника тока равно:
Лампа и резистор соединены последовательно и подключены к источнику постоянного тока. Сопротивление лампы в 10 раз больше, чем сопротивление резистора. Если напряжение на лампе Uл = 100 В, то напряжение напряжение U на зажимах источника тока равно:
Четыре резистора, сопротивления которых R1 = 2,0 Ом, R2 = 3,0 Ом, R3 = 4,0 Ом и R4= 1,0 Ом, соединены последовательно и подключены к источнику постоянного напряжения. Если напряжение на резисторе R1 составляет U1= 1,2 В, то напряжение U на клеммах источника равно:
Если общее сопротивление двух параллельно соединённых одинаковых резисторов R1 = 4 Ом, то общее сопротивление R2 этих же резисторов, соединённых последовательно, равно:
Если общее сопротивление двух параллельно соединённых одинаковых резисторов R1 = 6 Ом, то общее сопротивление R2 этих же резисторов, соединённых последовательно, равно:
На рисунке изображена схема электрической цепи, состоящей из резистора с сопротивлением R и реостата с максимальным сопротивлением 2R, подключённой к источнику постоянного напряжения U. Ползунок реостата находится в среднем положении, и в реостате выделяется тепловая мощность P1 = 90 Вт. Если ползунок реостата установить в крайнее правое положение, то тепловая мощность P2, выделяемая в реостате, станет равна:
На рисунке изображена схема электрической цепи, состоящей из резистора с сопротивлением R и реостата с максимальным сопротивлением R, подключённой к источнику постоянного напряжения U. Ползунок реостата находится в среднем положении, и в реостате выделяется тепловая мощность P1 = 96 Вт. Если ползунок реостата установить в крайнее правое положение, то тепловая мощность P2, выделяемая в реостате, станет равна:
Если при захвате ядром изотопа азота ![]() некоторой частицы образуются ядро изотопа кислорода
некоторой частицы образуются ядро изотопа кислорода ![]() и протон, то захваченной частицей является:
и протон, то захваченной частицей является:
На рисунке представлена схема электрической цепи, состоящей из источника тока, ключа и трех резисторов, сопротивления которых R1 = R2 = 4,00 Ом, R3 = 2,00 Ом. По цепи в течение промежутка времени t = 20,0 с проходит электрический ток. Если ЭДС источника тока ε = 12,0 В, а его внутреннее сопротивление r = 2,00 Ом, то полезная работа Aполезн. тока на внешнем участке цепи при разомкнутом ключе К равна ... Дж.
На рисунке представлена схема электрической цепи, состоящей из источника тока, ключа и трех резисторов, сопротивления которых R1 = R2 = 6,00 Ом, R3 = 2,00 Ом. По цепи в течение промежутка времени t = 30,0 с проходит электрический ток. Если ЭДС источника тока ε = 12,0 В, а его внутреннее сопротивление r = 1,00 Ом, то работа Aст. сторонних сил источника тока при разомкнутом ключе К равна ... Дж.
На рисунке представлена схема электрической цепи, состоящей из источника тока, ключа и трех резисторов, сопротивления которых R1 = R2 = 8,00 Ом, R3 = 4,00 Ом. По цепи в течение промежутка времени t = 25,0 с проходит электрический ток. Если ЭДС источника тока ε = 18,0 В, а его внутреннее сопротивление r = 2,00 Ом, то полезная работа Aполезн. тока на внешнем участке цепи при замкнутом ключе К равна ... Дж.
Электрическая цепь состоит из источника постоянного тока с ЭДС
![]() = 120 В и с внутренним сопротивлением r = 2,0 Ом, конденсатора ёмкостью С = 0,60 мкФ и двух резисторов (см. рис.). Если сопротивления резисторов R1 = R2 = 5,0 Ом, то заряд q конденсатора равен ... мкКл.
= 120 В и с внутренним сопротивлением r = 2,0 Ом, конденсатора ёмкостью С = 0,60 мкФ и двух резисторов (см. рис.). Если сопротивления резисторов R1 = R2 = 5,0 Ом, то заряд q конденсатора равен ... мкКл.
Электрическая цепь состоит из источника постоянного тока, конденсатора ёмкостью С = 6,0 мкФ и двух резисторов, сопротивления которых R1 = R2 = 5,0 Ом (см. рис.). Если внутреннее сопротивление источника r = 2,0 Ом, а заряд конденсатора q = 180 мкКл, то ЭДС источника тока
![]() равна ... В.
равна ... В.
Электрическая цепь состоит из источника постоянного тока, конденсатора ёмкостью С = 6,0 мкФ и двух резисторов, сопротивления которых R1 = R2 = 6,0 Ом (см. рис.). Если внутреннее сопротивление источника r = 2,0 Ом, а заряд конденсатора q = 180 мкКл, то ЭДС источника тока
![]() равна ... В.
равна ... В.
Электрическая цепь состоит из источника постоянного тока с ЭДС
![]() = 70 В, конденсатора ёмкостью С = 7,0 мкФ и двух резисторов, сопротивления которых R1 = R2 = 60 Ом (см. рис.). Если заряд конденсатора q = 210 мкКл, то внутреннее сопротивление источника r равно ... Ом.
= 70 В, конденсатора ёмкостью С = 7,0 мкФ и двух резисторов, сопротивления которых R1 = R2 = 60 Ом (см. рис.). Если заряд конденсатора q = 210 мкКл, то внутреннее сопротивление источника r равно ... Ом.
Электрическая цепь состоит из источника постоянного тока с ЭДС
![]() = 120 В, конденсатора ёмкостью С = 0,70 мкФ и двух резисторов, сопротивления которых R1 = R2 = 5,0 Ом (см. рис.). Если внутреннее сопротивление источника r = 2,0 Ом, то заряд q конденсатора равен ... мкКл.
= 120 В, конденсатора ёмкостью С = 0,70 мкФ и двух резисторов, сопротивления которых R1 = R2 = 5,0 Ом (см. рис.). Если внутреннее сопротивление источника r = 2,0 Ом, то заряд q конденсатора равен ... мкКл.
Электрическая цепь состоит из источника постоянного тока с ЭДС
![]() = 60 В и с внутренним сопротивлением r = 3,0 Ом, двух резисторов и конденсатора ёмкостью С = 0,50 мкФ (см. рис.). Если сопротивления резисторов R1 = R2 = 6,0 Ом, то заряд q конденсатора равен ... мкКл.
= 60 В и с внутренним сопротивлением r = 3,0 Ом, двух резисторов и конденсатора ёмкостью С = 0,50 мкФ (см. рис.). Если сопротивления резисторов R1 = R2 = 6,0 Ом, то заряд q конденсатора равен ... мкКл.
В электрической цепи, схема которой приведена на рисунке, сопротивления всех резисторов одинаковы и равны R, а внутреннее сопротивление источника тока пренебрежимо мало. Если до замыкания ключа K идеальный амперметр показывал силу тока I1 = 15 мА, то после замыкания ключа K амперметр покажет силу тока I2, равную ... мА.
В электрической цепи, схема которой приведена на рисунке, сопротивления всех резисторов одинаковы и равны R, а внутреннее сопротивление источника тока пренебрежимо мало. Если после замыкания ключа K идеальный амперметр показывал силу тока I2 = 64 мА, то до замыкания ключа K амперметр показывал силу тока I1, равную ... мА.
В электрической цепи, схема которой приведена на рисунке, сопротивления всех резисторов одинаковы и равны R, а внутреннее сопротивление источника тока пренебрежимо мало. Если до замыкания ключа K идеальный амперметр показывал силу тока I1 = 12 мА, то после замыкания ключа K амперметр покажет силу тока I2, равную ... мА.
В электрической цепи, схема которой приведена на рисунке, сопротивления всех резисторов одинаковы и равны R, а внутреннее сопротивление источника тока пренебрежимо мало. Если после замыкания ключа K идеальный амперметр показывал силу тока I2 = 98 мА, то до замыкания ключа K амперметр показывал силу тока I1, равную ... мА.
В электрической цепи, схема которой приведена на рисунке, сопротивления всех резисторов одинаковы и равны R, а внутреннее сопротивление источника тока пренебрежимо мало. Если после замыкания ключа K идеальный амперметр показывал силу тока I2 = 42 мА, то до замыкания ключа K амперметр показывал силу тока I1, равную ... мА.
Аккумулятор, ЭДС которого ![]() = 1,6 В и внутреннее сопротивление r = 0,1 Ом, замкнут нихромовым (с = 0,46 кДж/(кг · К) проводником массой m = 31,3 г. Если на нагревание проводника расходуется α = 75% выделяемой в проводнике энергии, то максимально возможное изменение температуры ΔTmax проводника за промежуток времени Δt = 1 мин равно ... К.
= 1,6 В и внутреннее сопротивление r = 0,1 Ом, замкнут нихромовым (с = 0,46 кДж/(кг · К) проводником массой m = 31,3 г. Если на нагревание проводника расходуется α = 75% выделяемой в проводнике энергии, то максимально возможное изменение температуры ΔTmax проводника за промежуток времени Δt = 1 мин равно ... К.
Аккумулятор, ЭДС которого ε = 1,5 В и внутреннее сопротивление r = 0,1 Ом, замкнут нихромовым (с = 0,46 кДж/(кг · К) проводником массой m = 40 г. Если на нагревание проводника расходуется α = 60% выделяемой в проводнике энергии, то максимально возможное изменение температуры ΔTmax проводника за промежуток времени Δt = 1 мин равно ... К.
Аккумулятор, ЭДС которого ε = 1,4 В и внутреннее сопротивление r = 0,1 Ом, замкнут нихромовым (с = 0,46 кДж/(кг · К) проводником массой m = 21,3 г. Если на нагревание проводника расходуется α = 60% выделяемой в проводнике энергии, то максимально возможное изменение температуры ΔTmax проводника за промежуток времени Δt = 1 мин равно ... К.
Аккумулятор, ЭДС которого ε = 1,5 В и внутреннее сопротивление r = 0,1 Ом, замкнут нихромовым (с = 0,46 кДж/(кг · К) проводником массой m = 36,6 г. Если на нагревание проводника расходуется α = 60% выделяемой в проводнике энергии, то максимально возможное изменение температуры ΔTmax проводника за промежуток времени Δt = 1 мин равно ... К.
Аккумулятор, ЭДС которого ε = 1,6 В и внутреннее сопротивление r = 0,1 Ом, замкнут нихромовым (с = 0,46 кДж/(кг · К) проводником массой m = 39,1 г. Если на нагревание проводника расходуется α = 75% выделяемой в проводнике энергии, то максимально возможное изменение температуры ΔTmax проводника за промежуток времени Δt = 1 мин равно ... К.
Сила тока в резисторе сопротивлением R = 16 Ом зависит от времени t по закону 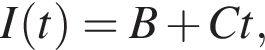 где B = 6,0 A,
где B = 6,0 A, 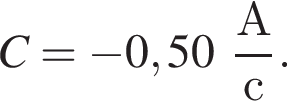 В момент времени
В момент времени 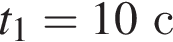 тепловая мощность P, выделяемая в резисторе, равна ... Вт.
тепловая мощность P, выделяемая в резисторе, равна ... Вт.
Если за время Δt = 30 суток показания счётчика электроэнергии в квартире увеличились на ΔW = 31,7 кВт · ч, то средняя мощность P, потребляемая электроприборами в квартире, равна ... Вт.
Если за время Δt = 30 суток показания счётчика электроэнергии в квартире увеличились на ΔW = 27,4 кВт · ч, то средняя мощность P, потребляемая электроприборами в квартире, равна ... Вт.
Нагревательный элемент сопротивлением R = 8,0 Ом подключён к источнику постоянного тока, коэффициент полезного действия которого ![]() = 80 % при данной нагрузке. При этом мощность нагревательного элемента составляет Р = 32 Вт. ЭДС
= 80 % при данной нагрузке. При этом мощность нагревательного элемента составляет Р = 32 Вт. ЭДС ![]() источника равна ... В.
источника равна ... В.
Участок цепи, состоящий из четырех резисторов (см. рис.), сопротивления которых R1 = 10,0 Ом, R2 = 20,0 Ом, R3 = 30,0 Ом и R4 = 40,0 Ом, подключен к источнику тока с ЭДС ε = 20,0 В и внутренним сопротивлением r = 20,0 Ом. Тепловая мощность P4, выделяемая в резисторе R4, равна ... мВт.
Участок цепи, состоящий из четырех резисторов (см. рис.), сопротивления которых R1 = 5,0 Ом, R2 = 10,0 Ом, R3 = 15,0 Ом и R4 = 20,0 Ом, подключен к источнику тока с ЭДС ε = 10,0 В и внутренним сопротивлением r = 10,0 Ом. Тепловая мощность P1, выделяемая в резисторе R1, равна ... мВт.
Участок цепи, состоящий из четырех резисторов (см. рис.), сопротивления которых R1 = 1,0 Ом, R2 = 2,0 Ом, R3 = 3,0 Ом и R4 = 4,0 Ом, подключен к источнику тока с ЭДС ε = 20,0 В и внутренним сопротивлением r = 2,0 Ом. Тепловая мощность P3, выделяемая в резисторе R3, равна ... Вт.
Троллейбус массой m = 12 т движется по горизонтальному участку дороги прямолинейно и равномерно. Коэффициент полезного действия двигателя троллейбуса ![]() = 82 %. Напряжение на двигателе троллейбуса U = 550 В, а сила тока в двигателе I = 35 А. Если отношение модулей силы сопротивления движению и силы тяжести, действующих на троллейбус,
= 82 %. Напряжение на двигателе троллейбуса U = 550 В, а сила тока в двигателе I = 35 А. Если отношение модулей силы сопротивления движению и силы тяжести, действующих на троллейбус, 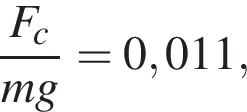 то модуль скорости троллейбуса равен....
то модуль скорости троллейбуса равен....![]()
В электрической цепи, схема которой приведена на рисунке, сопротивления всех резисторов одинаковы и равны R, а внутреннее сопротивление источника тока пренебрежимо мало. Если после замыкания ключа К идеальный амперметр показывает силу тока I2 = 28 мА, то до замыкания ключа К амперметр показывал силу тока I1 равную ... мА.
В электрической цепи, схема которой приведена на рисунке, сопротивления всех резисторов одинаковы и равны R, а внутреннее сопротивление источника тока пренебрежимо мало. Если до замыкания ключа К идеальный амперметр показывает силу тока I1 = 18 мА, то после замыкания ключа К амперметр показывал силу тока I2 равную ... мА.
Электрическая цепь состоит из источника постоянного тока с ЭДС
![]() = 300 В, двух резисторов сопротивлениями R1 = 100 Ом, R2 = 200 Ом и конденсатора ёмкостью C = 10 мкФ (см. рис.). В начальный момент времени ключ К был замкнут и в цепи протекал постоянный ток. Если внутренним сопротивлением источника тока пренебречь, то после размыкания ключа К на резисторе R2 выделится количество теплоты Q, равное ... мДж
= 300 В, двух резисторов сопротивлениями R1 = 100 Ом, R2 = 200 Ом и конденсатора ёмкостью C = 10 мкФ (см. рис.). В начальный момент времени ключ К был замкнут и в цепи протекал постоянный ток. Если внутренним сопротивлением источника тока пренебречь, то после размыкания ключа К на резисторе R2 выделится количество теплоты Q, равное ... мДж
В электрической цепи, схема которой представлена на рисунке, ёмкости конденсаторов C1 = 100 мкФ, C2 = 300 мкФ, ЭДС источника тока
 Сопротивление резистора R2 в два раза больше сопротивления резистора R1, то есть R2 = 2R1. В начальный момент времени ключ K замкнут и через резисторы протекает постоянный ток. Если внутреннее сопротивление источника тока пренебрежимо мало, то после размыкания ключа K в резисторе R2 выделится количество теплоты Q2, равное ... мДж.
Сопротивление резистора R2 в два раза больше сопротивления резистора R1, то есть R2 = 2R1. В начальный момент времени ключ K замкнут и через резисторы протекает постоянный ток. Если внутреннее сопротивление источника тока пренебрежимо мало, то после размыкания ключа K в резисторе R2 выделится количество теплоты Q2, равное ... мДж.
В электрической цепи, схема которой представлена на рисунке, ёмкости конденсаторов C1 = 40 мкФ, C2 = 120 мкФ, ЭДС источника тока ε = 90,0 В. Сопротивление резистора R2 в два раза больше сопротивления резистора R1, то есть R2 = 2R1. В начальный момент времени ключ K замкнут и через резисторы протекает постоянный ток. Если внутреннее сопротивление источника тока пренебрежимо мало, то после размыкания ключа K в резисторе R2 выделится количество теплоты Q2, равное ... мДж.
В электрической цепи, схема которой представлена на рисунке, ёмкости конденсаторов C1 = 400 мкФ, C2 = 300 мкФ, ЭДС источника тока
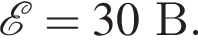 Сопротивление резистора R2 в два раза больше сопротивления резистора R1, то есть R2 = 2R1. В начальный момент времени ключ K замкнут и через резисторы протекает постоянный ток. Если внутреннее сопротивление источника тока пренебрежимо мало, то после размыкания ключа K в резисторе R2 выделится количество теплоты Q2, равное ... мДж.
Сопротивление резистора R2 в два раза больше сопротивления резистора R1, то есть R2 = 2R1. В начальный момент времени ключ K замкнут и через резисторы протекает постоянный ток. Если внутреннее сопротивление источника тока пренебрежимо мало, то после размыкания ключа K в резисторе R2 выделится количество теплоты Q2, равное ... мДж.
На рисунке представлена схема электрической цепи, состоящей из конденсатора, ключа и двух резисторов, сопротивления которых R1 = 1 МОм и R2 = 2 МОм. Если электрическая емкость конденсатора С = 1 нФ, а его заряд q = 6 мкКл, то количество теплоты Q1 которое выделится в резисторе R1 при полной разрядке конденсатора после замыкания ключа К, равно ... мДж.
На рисунке представлена схема электрической цепи, состоящей из конденсатора, ключа и двух резисторов, сопротивления которых R1 = 4,0 МОм и R2 = 2,0 МОм. Если электрическая емкость конденсатора С = 1,5 нФ, а его заряд q = 18 мкКл, то количество теплоты Q2 которое выделится в резисторе R2 при полной разрядке конденсатора после замыкания ключа К, равно ... мДж.
На рисунке представлена схема электрической цепи, состоящей из конденсатора, ключа и двух резисторов, сопротивления которых R1 = 6,0 МОм и R2 = 3,0 МОм. Если электрическая емкость конденсатора С = 1,0 нФ, а его заряд q = 9,0 мкКл, то количество теплоты Q1 которое выделится в резисторе R1 при полной разрядке конденсатора после замыкания ключа К, равно ... мДж.
Две лёгкие спицы одинаковой длины h и стержень массой m и длиной L = 20 см образуют П-образный (прямоугольный) проводник CDEF, который может свободно вращаться вокруг горизонтальной оси OO'. Проводник помещён в однородное магнитное поле, модуль индукции которого B = 100 мТл, а линии индукции направлены вертикально вверх (см. рис.). В проводнике протекает постоянный ток I = 39 А. Проводник отклонили так, что его плоскость стала горизонтальной, а затем отпустили без начальной скорости. Если мгновенная скорость стержня стала равной нулю в тот момент, когда угол между плоскостью проводника и горизонтом
![]() = 30°, то масса m стержня равна ... г.
= 30°, то масса m стержня равна ... г.
На рисунке изображён участок цепи, в котором сопротивления всех резисторов одинаковы. Вольтметр с бесконечно большим сопротивлением, подключённый к точкам 1 и 2, показывает напряжение U12 = 34 В. Если вольтметр отключить от точки 2 и подключить к точке 3, то его показания U13 будут равны ... B.
На рисунке изображён участок цепи, в котором сопротивления всех резисторов одинаковы. Вольтметр с бесконечно большим сопротивлением, подключённый к точкам 1 и 2, показывает напряжение U12 = 42 В. Если вольтметр отключить от точки 1 и подключить к точке 3, то его показания U23 будут
На рисунке изображена электрическая цепь, подключённая к источнику постоянного напряжения с пренебрежимо малым внутренним сопротивлением. Сопротивления каждого резистора и всей намотки реостата одинаковы, амперметр — идеальный. Если ЭДС источника
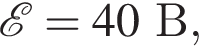 то после перемещения ползунка реостата из среднего положения в крайнее левое положение во внешней цепи будет выделяться тепловая мощность P,
то после перемещения ползунка реостата из среднего положения в крайнее левое положение во внешней цепи будет выделяться тепловая мощность P,
Проводник, вольт-амперная характеристика которого показана на рисунке, и резистор соединены последовательно и подключены к источнику постоянного тока. Если сопротивление резистора R = 5,0 Ом, а сила тока в цепи I = 2,5 A , то напряжение U на клеммах источника тока равно ... B.
Правильное соотношение между работой A электрического тока на участке цепи, силой тока I в цепи, временем t прохождения тока по участку цепи, а также напряжением U на этом участке цепи указано под номером:



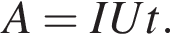
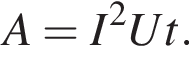
Проводник, вольт-амперная характеристика которого показана на рисунке, и резистор соединены последовательно и подключены к источнику постоянного тока, напряжение на клеммах которого U = 7,5 В. Если напряжение на резисторе UR = 2,5 В, то сила тока I в цепи

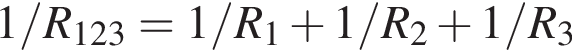
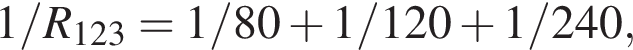
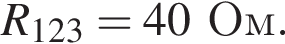
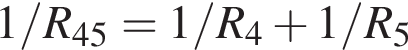
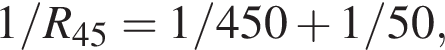

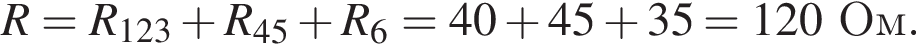
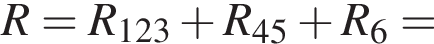
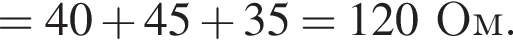
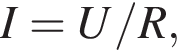
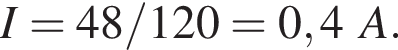

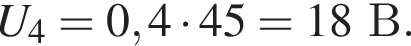



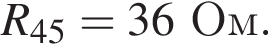

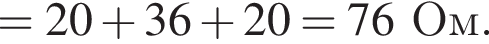


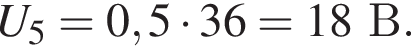


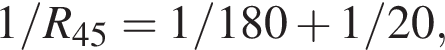
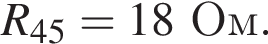
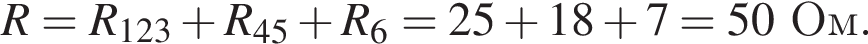
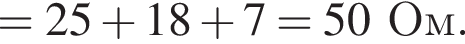
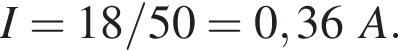

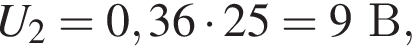

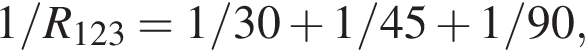
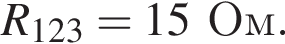
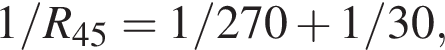
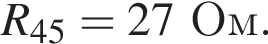
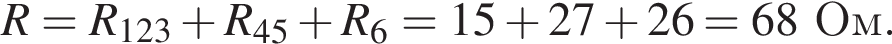
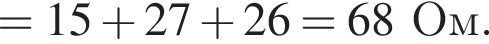
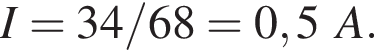

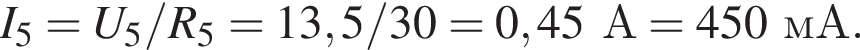



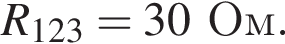
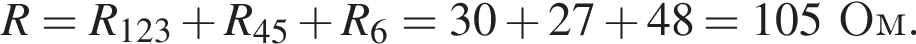
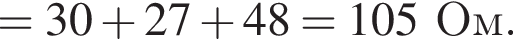
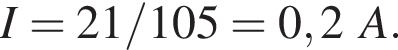

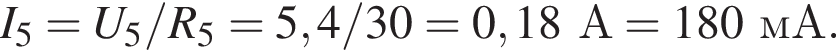
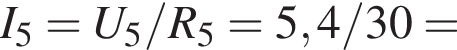

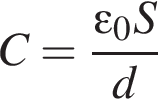 уменьшится в 3 раза. Из формулы энергии заряженного конденсатора
уменьшится в 3 раза. Из формулы энергии заряженного конденсатора 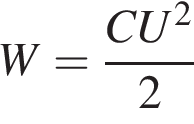 следует, что энергия уменьшится в 3 раза.
следует, что энергия уменьшится в 3 раза.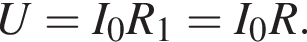 Сила тока, протекающего через резистор
Сила тока, протекающего через резистор 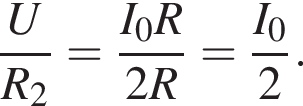 Такая же сила тока, протекающего через резистор
Такая же сила тока, протекающего через резистор 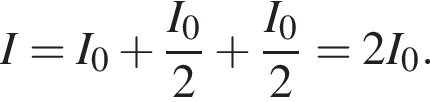
 где I — сила тока в цепи, равная
где I — сила тока в цепи, равная 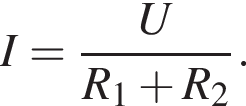 С учётом
С учётом  получаем:
получаем: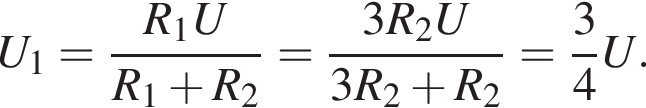
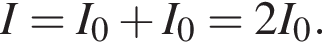
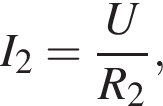 где I — сила тока в цепи, равная
где I — сила тока в цепи, равная 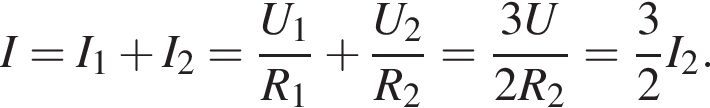
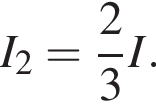
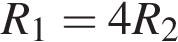 получаем:
получаем: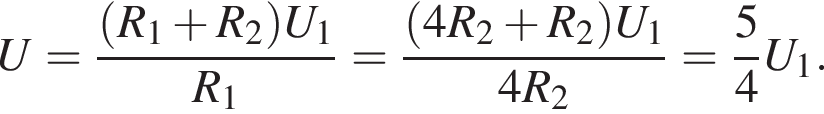
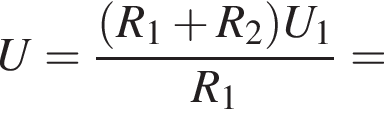
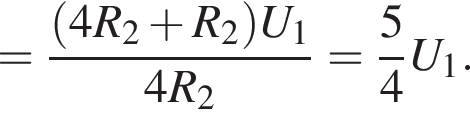
 Протекающий через источник ток является суммой токов на всех резисторах, который вычисляется по закону Ома:
Протекающий через источник ток является суммой токов на всех резисторах, который вычисляется по закону Ома: 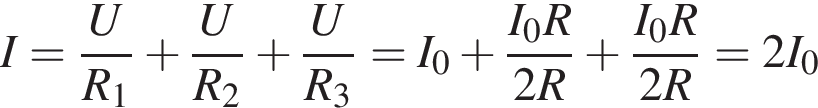
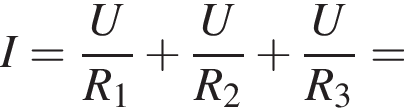
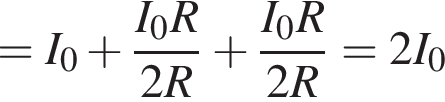
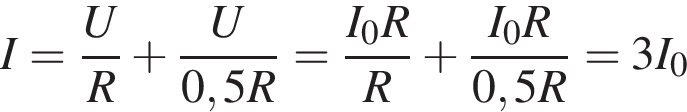
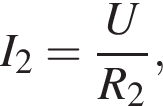 где I — сила тока в цепи, равная
где I — сила тока в цепи, равная 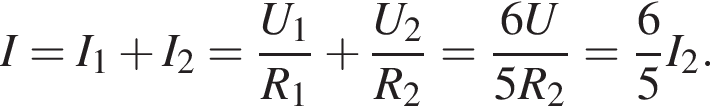
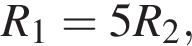
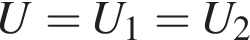 получаем:
получаем: 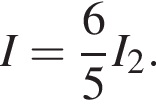
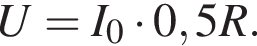 Протекающий через источник ток является суммой токов на всех резисторах, который вычисляется по закону Ома:
Протекающий через источник ток является суммой токов на всех резисторах, который вычисляется по закону Ома: 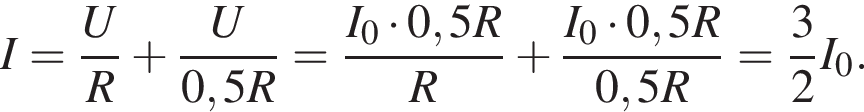
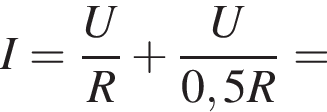
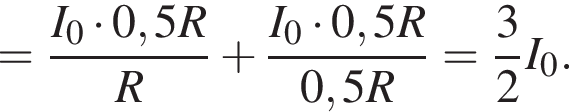
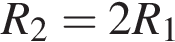 получаем:
получаем: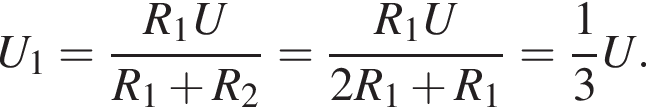
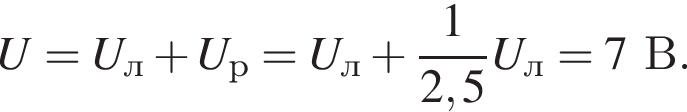
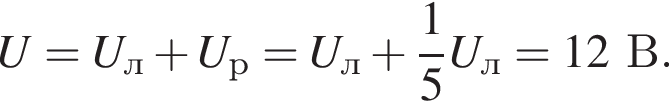
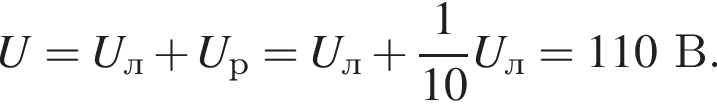
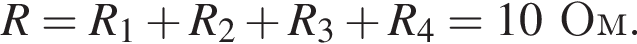 Через резистор
Через резистор 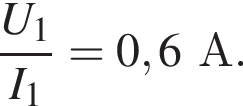 Таким образом, через подключённый к источнику участок цепи общим сопротивлением 10 Ом течёт ток силой 0,6 А. Напряжение на клеммах источника по закону Ома равно
Таким образом, через подключённый к источнику участок цепи общим сопротивлением 10 Ом течёт ток силой 0,6 А. Напряжение на клеммах источника по закону Ома равно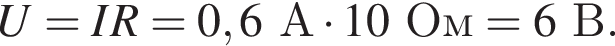
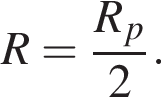 Тогда сопротивление резистора равно
Тогда сопротивление резистора равно  Ом.
Ом. Ом.
Ом.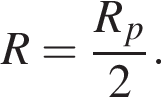 Тогда сопротивление резистора равно
Тогда сопротивление резистора равно  Ом
Ом Ом.
Ом.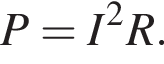
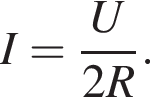 Тогда мощность, выделяющаяся на реостате, равна
Тогда мощность, выделяющаяся на реостате, равна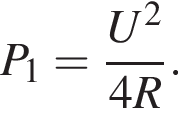
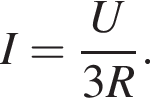 Тогда мощность, выделяющаяся на реостате, равна
Тогда мощность, выделяющаяся на реостате, равна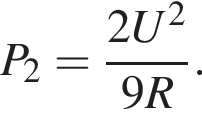
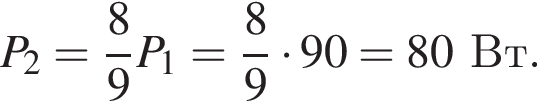
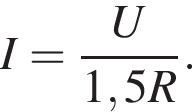 Тогда мощность, выделяющаяся на реостате, равна
Тогда мощность, выделяющаяся на реостате, равна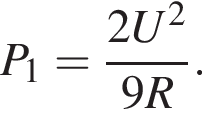
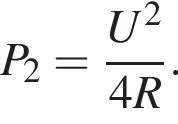
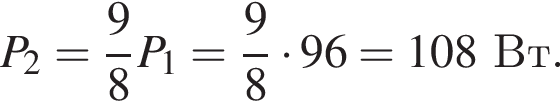
 Используя законы сохранения массы и заряда, находим, что А = 4, Z = 2, следовательно, захвачена альфа-частица.
Используя законы сохранения массы и заряда, находим, что А = 4, Z = 2, следовательно, захвачена альфа-частица.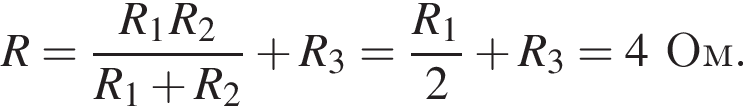
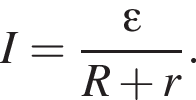
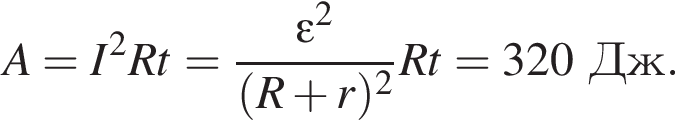
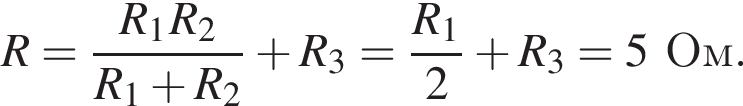
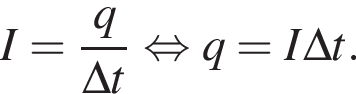
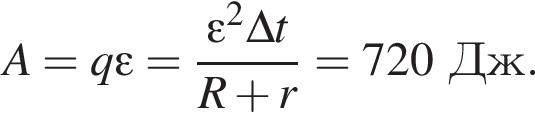
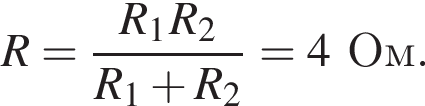
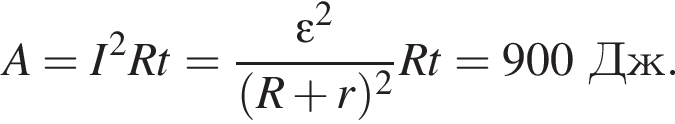
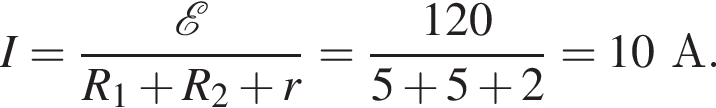
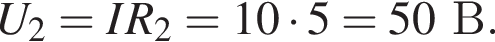 Заряд конденсатора равен
Заряд конденсатора равен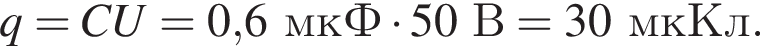
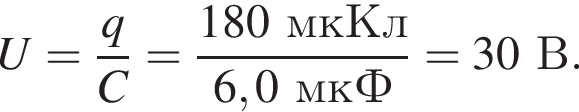
 Так как источник и два резистора образуют последовательную цепь (через конденсатор ток не течёт), то ток в цепи равен:
Так как источник и два резистора образуют последовательную цепь (через конденсатор ток не течёт), то ток в цепи равен: 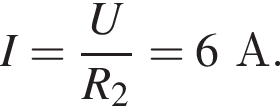
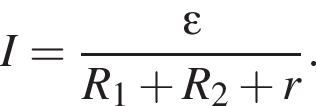
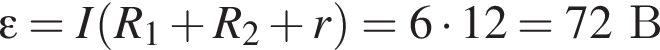
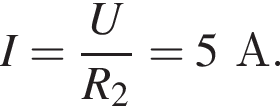
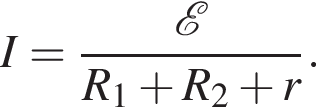
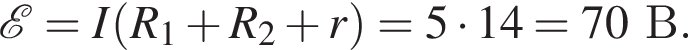
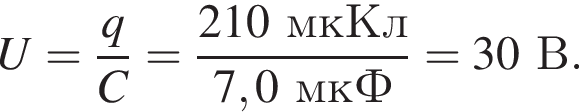
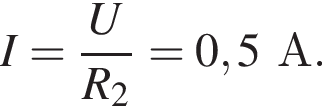
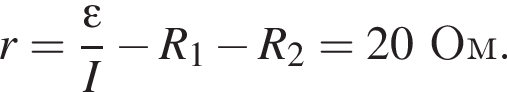
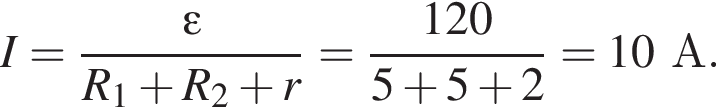
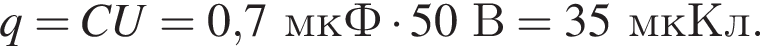
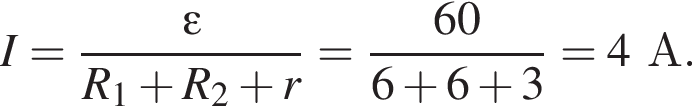
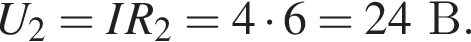 Заряд конденсатора равен
Заряд конденсатора равен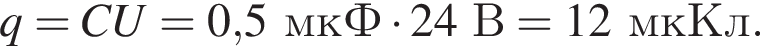
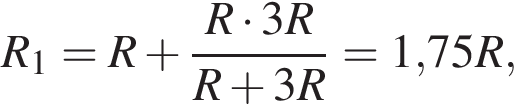 после замыкания —
после замыкания — 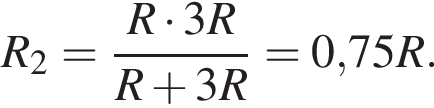 ЭДС не изменилась, поэтому
ЭДС не изменилась, поэтому  и значит:
и значит: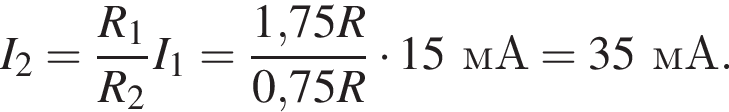
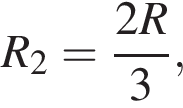 до замыкания —
до замыкания — 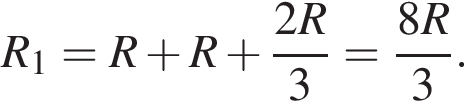 ЭДС не изменилась, поэтому
ЭДС не изменилась, поэтому 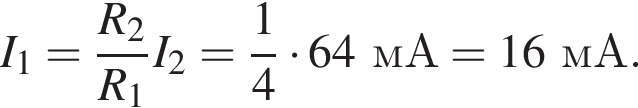
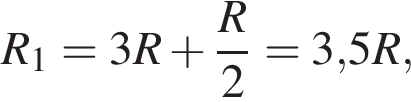 после замыкания —
после замыкания — 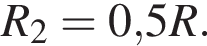 ЭДС не изменилась, поэтому
ЭДС не изменилась, поэтому 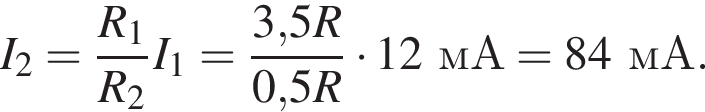
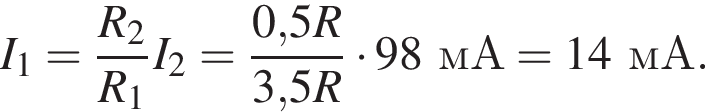
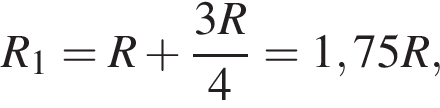 после замыкания —
после замыкания — 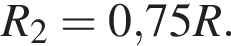 ЭДС не изменилась, поэтому
ЭДС не изменилась, поэтому 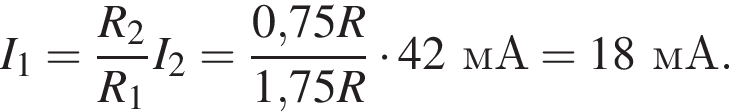
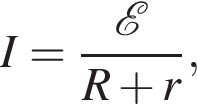
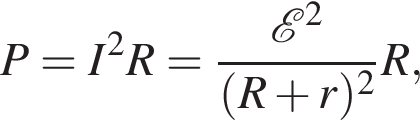
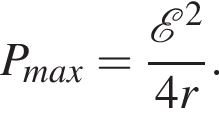
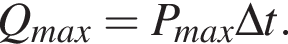

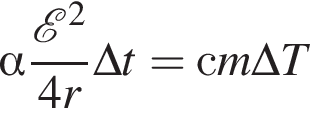
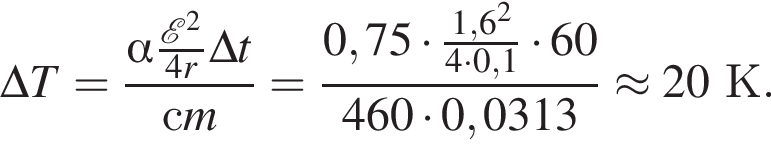
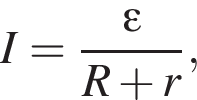
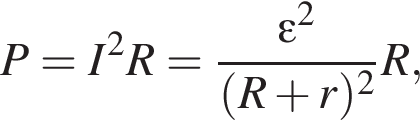
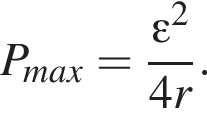

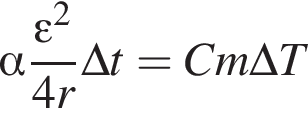
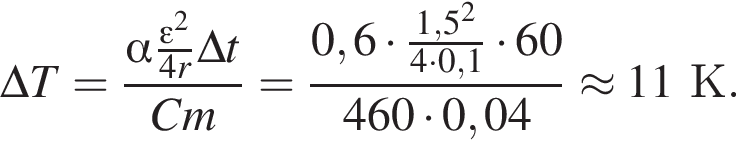
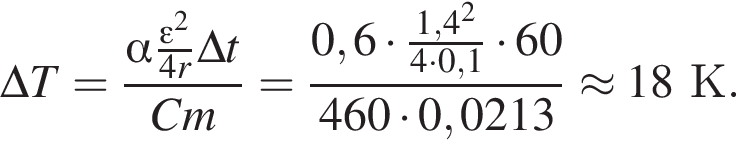
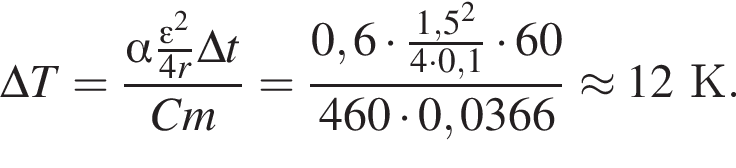

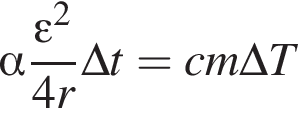
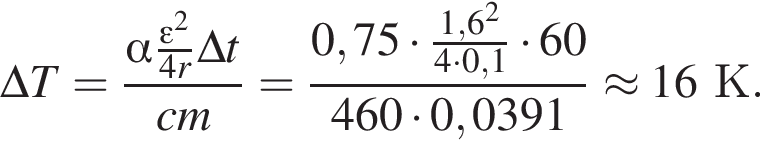
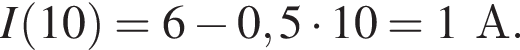
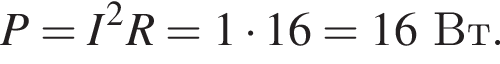
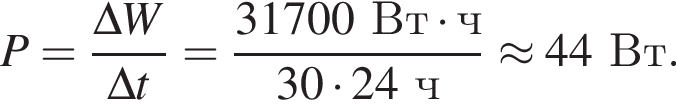
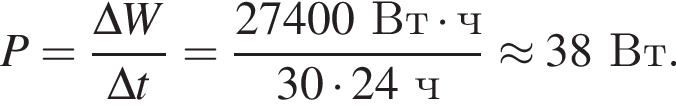

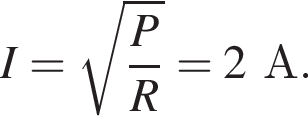
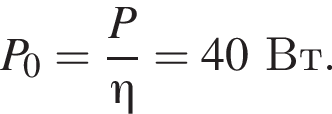 ЭДС равна
ЭДС равна 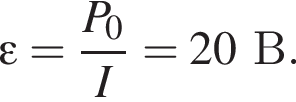
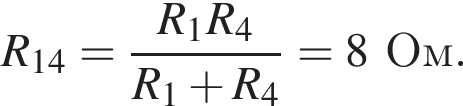
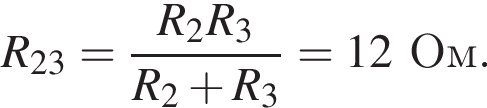
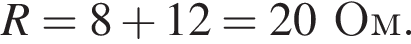
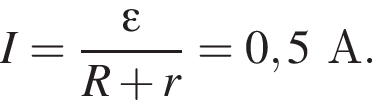
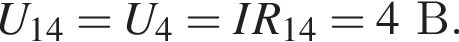
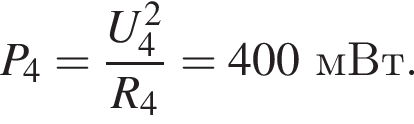
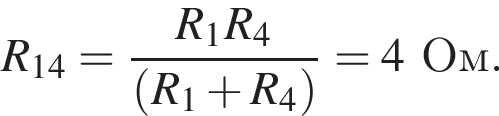
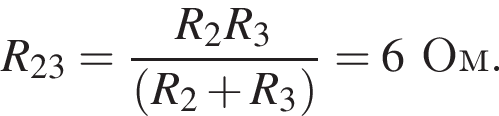

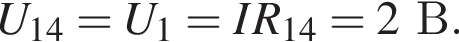
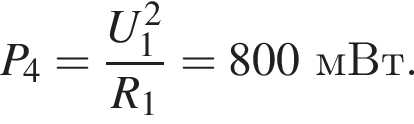
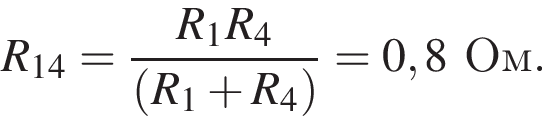
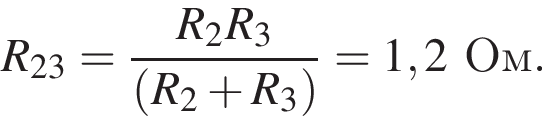
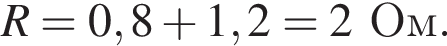
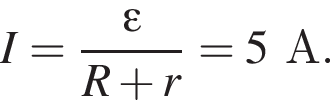
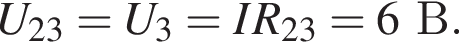
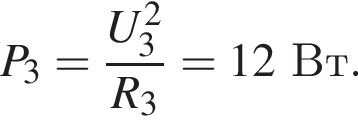
 Мощность, создаваемая двигателем
Мощность, создаваемая двигателем  В энергию движения переходит только часть полученной от двигателя энергии, соответственно, полезная мощность, уходящая на поддержание движения троллейбуса равна
В энергию движения переходит только часть полученной от двигателя энергии, соответственно, полезная мощность, уходящая на поддержание движения троллейбуса равна 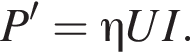 Пусть за время Δt троллейбус проходит расстояние ΔS. С одной стороны, энергия, получаемая троллейбусом от двигателя равна
Пусть за время Δt троллейбус проходит расстояние ΔS. С одной стороны, энергия, получаемая троллейбусом от двигателя равна 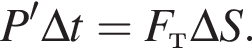 Заметим, что
Заметим, что 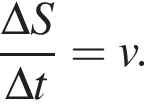 Найдём скорость троллейбуса:
Найдём скорость троллейбуса: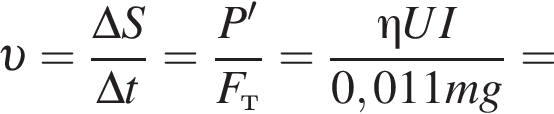
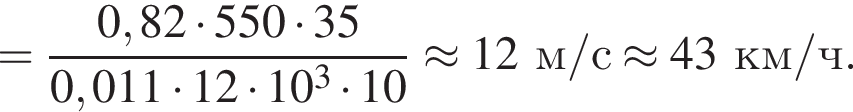
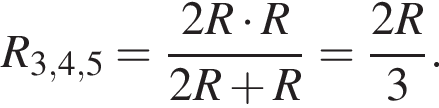 Общее сопротивление цепи
Общее сопротивление цепи 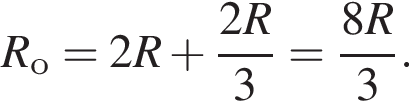
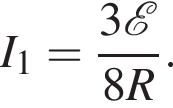 При замкнутом ключе ток пойдет по пути наименьшего сопротивления, и потому общее сопротивление цепи будет равно Rо = 2R, а сила тока
При замкнутом ключе ток пойдет по пути наименьшего сопротивления, и потому общее сопротивление цепи будет равно Rо = 2R, а сила тока 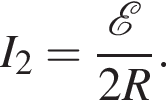 Таким образом,
Таким образом, 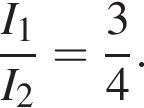 Откуда
Откуда 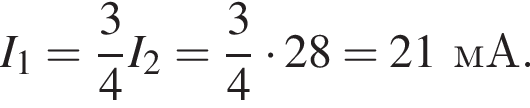
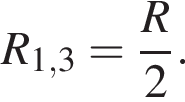 Аналогично резисторы 2 и 4 соединены параллельно и сопротивление участка так же
Аналогично резисторы 2 и 4 соединены параллельно и сопротивление участка так же 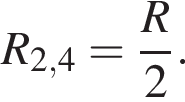 Эти участки соединены последовательно, поэтому R1,2,3,4 = R. Общее сопротивление цепи R0 = 2R. По закону Ома для полной цепи (учитывая, что внутренним сопротивлением можно пренебречь) сила тока равна
Эти участки соединены последовательно, поэтому R1,2,3,4 = R. Общее сопротивление цепи R0 = 2R. По закону Ома для полной цепи (учитывая, что внутренним сопротивлением можно пренебречь) сила тока равна 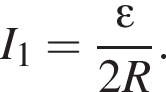
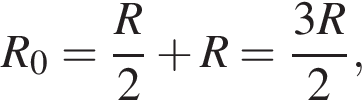
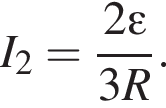 Таким образом,
Таким образом, 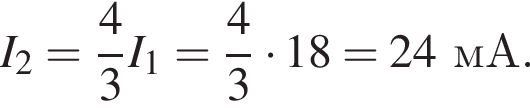
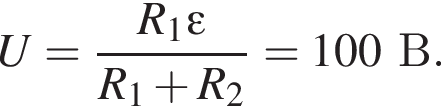 Заряд на нём равен
Заряд на нём равен 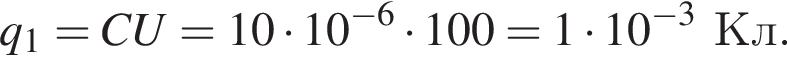 Энергия электрического поля в конденсаторе равна
Энергия электрического поля в конденсаторе равна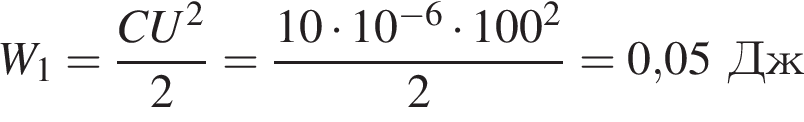
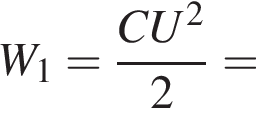
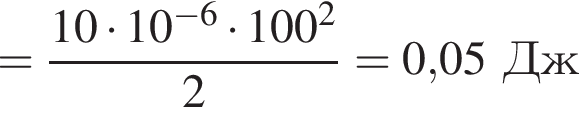
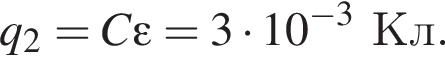 Энергия электрического поля в конденсаторе станет равной
Энергия электрического поля в конденсаторе станет равной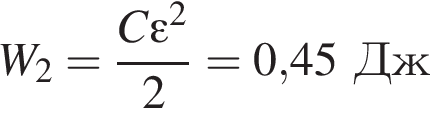
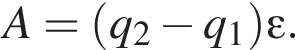 Часть этой работы пошла на увеличение энергии электрического поля в конденсаторе, часть выделилась в виде теплоты на резисторе:
Часть этой работы пошла на увеличение энергии электрического поля в конденсаторе, часть выделилась в виде теплоты на резисторе:
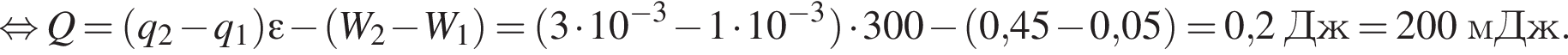
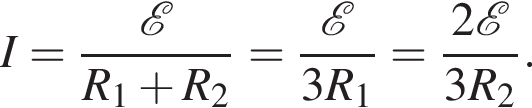
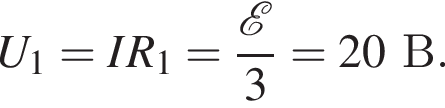
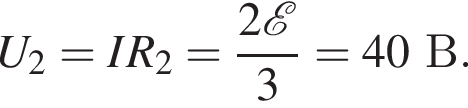
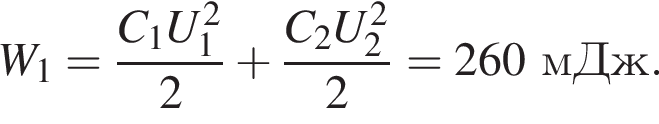
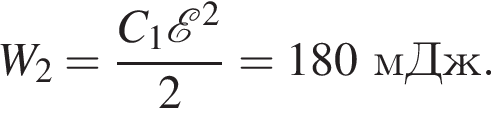

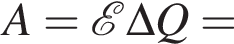
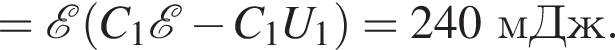

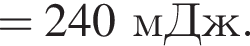
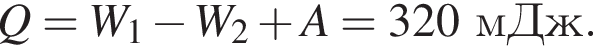
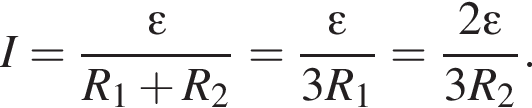
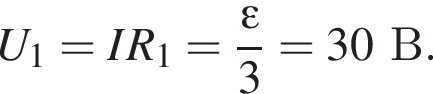
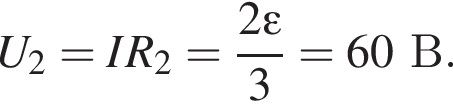
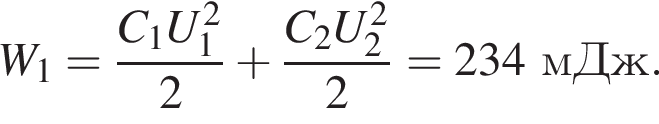
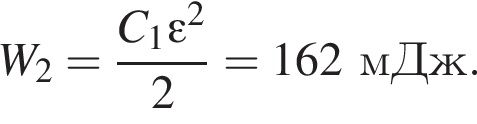
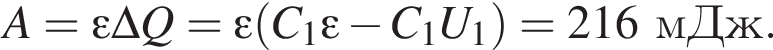
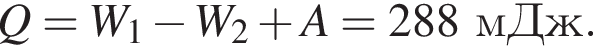
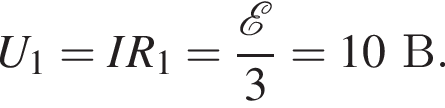
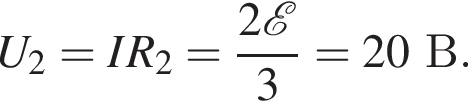
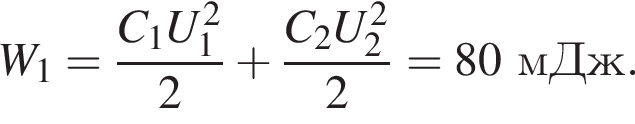
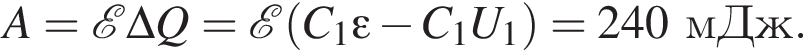
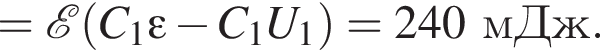
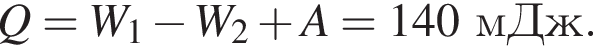
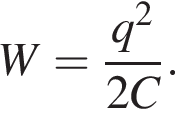
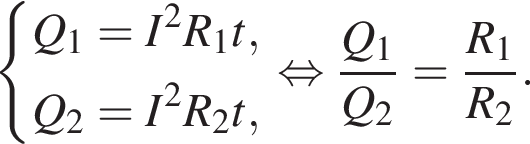
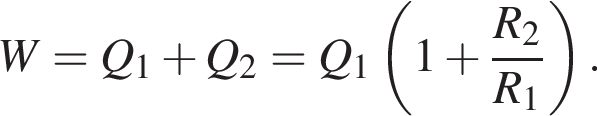
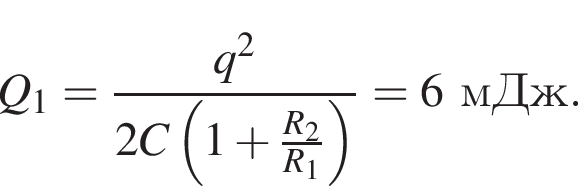
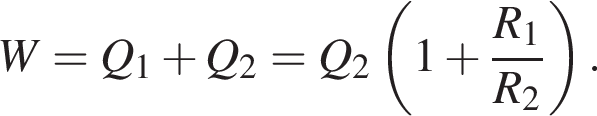
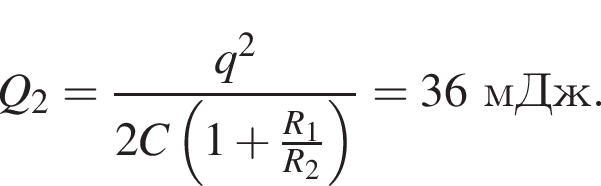
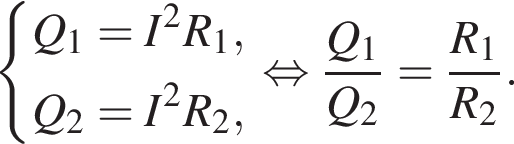
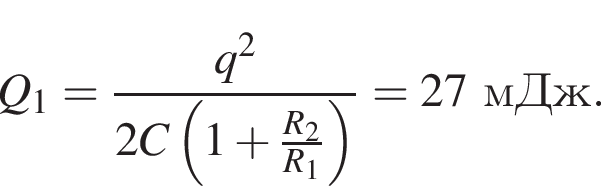
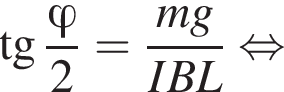
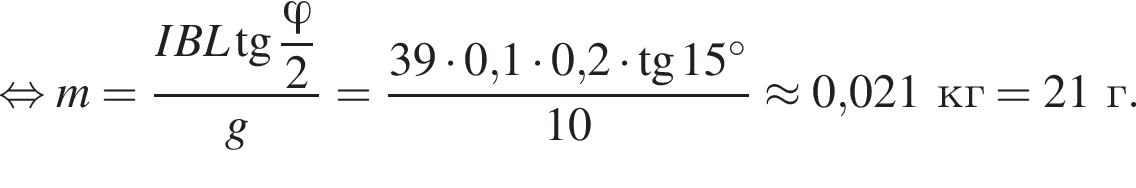
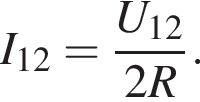
 сила тока через этот резистор равна
сила тока через этот резистор равна 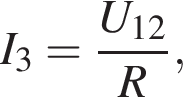 а общая сила тока
а общая сила тока 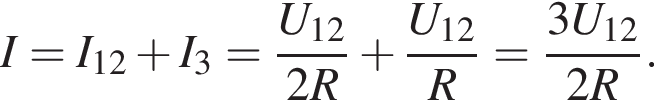
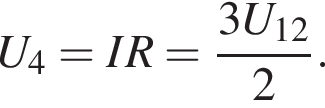 Следовательно, напряжение между точками 1 и 3 будет равным
Следовательно, напряжение между точками 1 и 3 будет равным 
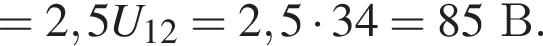
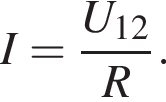
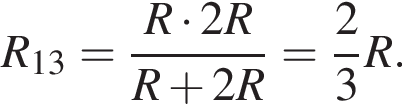
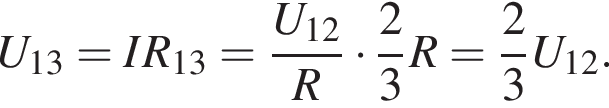
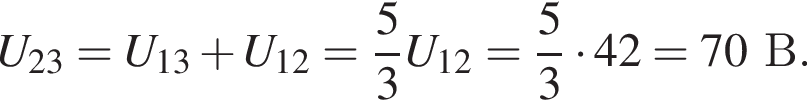
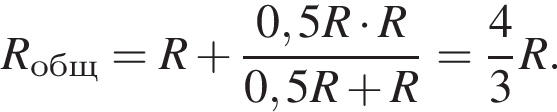
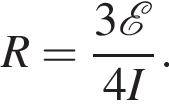
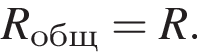 Тогда выделившаяся о внешней цепи мощность равна
Тогда выделившаяся о внешней цепи мощность равна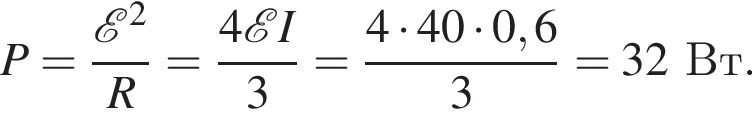
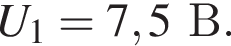 Найдем напряжение на резисторе, используя закон Ома для участка цепи:
Найдем напряжение на резисторе, используя закон Ома для участка цепи: